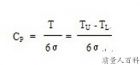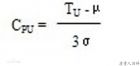CPK
过程能力指数是指过程能力满足产品质量标准要求(规格范围等)的程度。也称工序能力指数,是指工序在一定时间里,处于控制状态(稳定状态)下的实际加工能力。它是工序固有的能力,或者说它是工序保证质量的能力。这里所指的工序,是指操作者、机器、原材料、工艺方法和生产环境等五个基本质量因素综合作用的过程,也就是产品质量的生产过程。
术语定义
CPK:过程能力指数(Process capability index)表示过程能力满足技术标准(例如规格、公差)的程度。
计算公式
CPK= Min[ (USL- Mu)/3σ, (Mu - LSL)/3σ]
1、双侧规格
双侧规格情形的过程能力指数,这时,过程能力指数CP的计算公式如下:式中,T为过程统计量的技术规格的公差幅度;TU、TL分别为上、下公差界限;σ为过程统计量的总体标准差,可以在过程处于稳态时得到。
2、有偏移情形
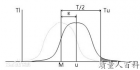
有偏移情形的过程能力指数:当过程统计量的分布均值μ与公差中心M不重合(即有偏移)时,如图1所示,显然不合格率(如图1上的PU)增大,也即CP值降低,故式(1)所计算的过程能力指数不能反映有偏移的实际情形,需要加以修正。定义分布的总体均值μ与公差中心M的偏移为ε=|M-μ|,μ与M的偏移度为K:
这样,当μ=M(即分布中心与公差中心重合,无偏移)时,K=0,则CPK=CP;而当μ=TU或μ=TL时,K=1,CPK=0,表示过程能力由于偏移而严重不足,需要采取措施加以纠正。显然,具有:CPK≤CP
3、单侧规格
式中,CPU为上单侧过程能力指数。若μ≥TU,令CPU=0,表示过程能力严重不足,过程的不合格品率高达50%以上。
运算方法
过程能力指数运算有5种计算方法:
直方图(两种绘图方法);
散布图(直线回归和曲线回归)(5种);
计算剩余标准差;排列图(自动检索和排序);
波动图(单边控制规范,也可以是双边控制规范)。
指标
Cp、Cpk
Cp是指过程满足技术要求的能力,常用客户满意的偏差范围除以六倍的西格玛的结果来表示。
T=允许最大值(Tu)-允许最小值(Tl)
Cp=T/(6*σ)
所以σ越小,其Cp值越大,则过程技术能力越好。
Cpk是指过程平均值与产品标准规格发生偏移(ε)的大小,常用客户满意的上限偏差值减去平均值和平均值减去下限偏差值中数值小的一个,再除以三倍的西格玛的结果来表示。
Cpk=MIN(Tu-μ,μ-Tl)/(3*σ)
或者Cpk=(1-k)*Cp,其中k=ε/(T/2)
通常状况下,质量特性值分布的总体标准差(σ)是未知的,所以应采用样本标准差(s)来代替。
Pp、Ppk
其公式同Cp、Cpk一样,但σ是全部样本的标准偏差,即等于所有样本的标准差S。
指数意义
1.67-2 过大,可适当放宽检验
1.33-1.67 充分,继续保持
1-1.33 正常,但接近1危险
小于1 不充分,需改进,严重时停产需整顿
说明
以上所提情况皆为正态情况下,当为非正态时情况则不同。
例如:某些产品的质量特性值是遵从指数分布的,Cp=T/(5.9*σ).过程能力指数, 制程准确度, 制程精密度三者的关系 Cpk = Cp * ( 1 - |Ca|)
Cpk是Ca及Cp两者的中和反应,Ca反应的是位置关系(居中趋势),Cp反应的是散布关系(离散趋势)
用途
工序能力是表示生产过程客观存在着分散的一个参数。但是这个参数能否满足产品的技术要求,仅从它本身还难以看出。因此,还需要另一个参数来反映工序能力满足产品技术要求(公差、规格等质量标准)的程度。这个参数就叫做工序能力指数,它是技术要求和工序能力的比值。
过程能力指数的值越大,表明产品的离散程度相对于技术标准的公差范围越小,因而过程能力就越高;过程能力指数的值越小,表明产品的离散程度相对公差范围越大,因而过程能力就越低。因此,可以从过程能力指数的数值大小来判断能力的高低。从经济和质量两方面的要求来看,过程能力指数值并非越大越好,而应在一个适当的范围内取值。 [2]
制程能力是过程性能的允许最大变化范围与过程的正常偏差的比值。
制程能力研究在於确认这些特性符合规格的程度,以保证制程成品不符规格的不良率在要求的水准之上,作为制程持续改善的依据。
当我们的测量系统通过了GageR&R的测试之后,我们即可开始Cpk值的测试。
CPK值越大表示生产工序过程保持稳定的能力越充足。
CPK=min((X-LSL/3s),(USL-X/3s))
应用
1 当选择制程站别Cpk来作管控时,应以成本做考量的首要因素,还有是其品质特性对后制程的影响度。
2. 计算取样数据至少应有20~25组数据,方具有一定代表性。
3. 计算Cpk除收集取样数据外,还应知晓该品质特性的规格上下限(USL,LSL),才可顺利计算其值。
4. 首先可用Excel的“STDEV”函数自动计算所取样数据的标准差(σ),再计算出规格公差(T),及规格中心值(u). 规格公差=规格上限-规格下限;规格中心值=(规格上限+规格下限)/2;
5. 依据公式:Ca=(X-U)/(T/2) , 计算出制程准确度:Ca值 (x为所有取样数据的平均值)
6. 依据公式:Cp =T/6σ , 计算出制程精密度:Cp值
7. 依据公式:Cpk=Cp(1-|Ca|) , 计算出制程能力指数:Cpk值
8. Cpk的评级标准:(可据此标准对计算出之制程能力指数做相应对策)
A++级 Cpk≥2.0 特优 可考虑成本的降低
A+ 级 2.0 > Cpk ≥ 1.67 优 应当保持之
A 级 1.67 > Cpk ≥ 1.33 良 能力良好,状态稳定,但应尽力提升为A+级
B 级 1.33 > Cpk ≥ 1.0 一般 状态一般,制程因素稍有变异即有产生不良的危险,应利用各种资源及方法将其提升为 A级
C 级 1.0 > Cpk ≥ 0.67 差 制程不良较多,必须提升其能力
D
| 评级 | 值 | 评价 |
|---|---|---|
| A++级 | Cpk≥2.0 | 特优 可考虑成本的降低 |
| A+ 级 | 2.0 > Cpk ≥ 1.67 | 优 应当保持之 |
| A 级 | 1.67 > Cpk ≥ 1.33 | 良 能力良好,状态稳定,但应尽力提升为A+级 |
| B 级 | | |
| C 级 | | |
| D 级 | 0.67 > Cpk | 不可接受 其能力太差,应考虑重新整改设计制程。 |
级 0.67 > Cpk 不可接受 其能力太差,应考虑重新整改设计制程。